【旧帝一工神】偏差値70keep☆Part4【医歯薬獣医】
最新 最初 全 
#1 [名前なし]
 :08/10/29 00:38
:08/10/29 00:38  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg
#2 [名前なし]
■■■ スレの方針 ■■■
◎対象の大学、学部は
>>1参照。
◎質問はできるだけ具体的に。答える側の身にもなって下さい!
◎問題のぅpもする。ただし難問はナシの方針で!
◎模試等の成績を載せる。どんなに悪くても載せる(笑)
対象となる大学志望者以外の人もいるので、モチベーション上げるために参加したい方などは要相談(゚Д゚)
ってワケで集まれ!(・∀・)
 :08/10/29 00:39
:08/10/29 00:39  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg
#3 [名前なし]
めんば~一覧(大学生混じってます)
名前/志望校/所属・学年
マメ/―/某旧帝大薬
タマ(ポチ)/―/某国立大教育
きいろいやつ/―/某国立大工
マイ/―/某旧帝大
シャイ/―/某旧帝大
あ/―/某旧帝大
心理/―/某私立大
ふわふわ/―/某旧帝大
きいろいとり/?/?
ばなな/―/某私立大
カセキ/―/某旧帝大
勇蔵/―/某私立大
うけにュ/―/大学生
й/東大理一/河合
みなみ/名市医/駿台
ジャス/一橋/河合
好位置/東大文一/高3
アヒャ/大分医/高3
あずさ/千葉大薬/高3
文佳/京府医/高3
りよ/名大か九大経済/高3
◆AKI/vCK/rA/千葉大薬/高3
ゆーこ/九大/高2
舞/佐賀医か九大医/高1
襟/70ぐらいの大学/高1
(2008.10.29時点)
 :08/10/29 00:39
:08/10/29 00:39  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg
#4 [名前なし]
終わった(´・ω・`)
 :08/10/29 00:40
:08/10/29 00:40  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg
#5 [めたぼりっくリんご ]
]
おつかれさまー(´^ω^`)
 :08/10/29 00:49
:08/10/29 00:49  :P905i
:P905i  :91Mltsbg
:91Mltsbg
#6 [ジャス]
お疲れさまですっ!
 :08/10/29 01:16
:08/10/29 01:16  :SO902i
:SO902i  :diGJk4Ss
:diGJk4Ss
#7 [ゆ-こ]
お疲れ様です★
久しぶりですね
九大はなんとかB判定がとれるようになりました(´`)
最近は第1志望を阪大にしてます♪
 :08/10/29 01:23
:08/10/29 01:23  :P703i
:P703i  :oZ762SKI
:oZ762SKI
#8 [名前なし]
お疲れ様です(^0_0^)
前スレにて参加表明をしようと思いましたが終わりそうでありましたので待っていました( ̄ω ̄)
高2で東北志望の淳です。よろしくお願いします(^.^)
 :08/10/29 10:24
:08/10/29 10:24  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆
#9 [メタボリックうけにュ◆orz/.UKENU]
お疲れさまです(。・ω・。)
 :08/10/29 10:59
:08/10/29 10:59  :N902i
:N902i  :rsnfemGo
:rsnfemGo
#10 [あひゃ]
乙ですo(^-^)o
ありがとうございます
 :08/10/29 21:37
:08/10/29 21:37  :SO903i
:SO903i  :iWa/ynxU
:iWa/ynxU
#11 [あひゃ]
次ここに来るのはセンター後だな(´-ω-`)
ノシ
 :08/10/29 21:39
:08/10/29 21:39  :SO903i
:SO903i  :iWa/ynxU
:iWa/ynxU
#12 [‰]
どもっ!
東大志望の高1です
参加させて下さ~い。
(´・ω・`)
 :08/10/29 22:20
:08/10/29 22:20  :P903i
:P903i  :V0FRtt76
:V0FRtt76
#13 [名前なし]
天才なら3年、いいぐらいなら2年、凡人なら1年から頑張れ。
 :08/10/29 22:45
:08/10/29 22:45  :SH903i
:SH903i  :t89fHafE
:t89fHafE
#14 [名前なし]
 :08/10/30 20:24
:08/10/30 20:24  :F703i
:F703i  :☆☆☆
:☆☆☆
#15 [名前なし]
高2までの範囲で解ける数学の難しい問題なんかありませんか?ありましたら解きたいので何問かください
 :08/10/30 23:21
:08/10/30 23:21  :SH703i
:SH703i  :☆☆☆
:☆☆☆
#16 [あ]
円周率が3.05以上であることを証明\(^_^)/
理三の人とかコマの歳差運動とか高二でやったみたいorz
 :08/10/31 06:46
:08/10/31 06:46  :W61H
:W61H  :udyzDCGM
:udyzDCGM
#17 [名前なし]
それ解いたことあります。でもありがとうございます
 :08/10/31 12:09
:08/10/31 12:09  :SH703i
:SH703i  :☆☆☆
:☆☆☆
#18 [あ]
レベル高そう(゜ω゜)
東大の過去問がいい?(^ω^)
 :08/10/31 13:58
:08/10/31 13:58  :W61H
:W61H  :udyzDCGM
:udyzDCGM
#19 [名前なし]
何日か前にやった問題を出してみるか‥うろ覚えだから間違ってたらすまん
nを正の整数、aを実数とする。すべての整数mに対してm^2-(a-1)m+{n^2/(2n+1)}a>0が成り立つようなaの範囲をnを用いて表せ
 :08/10/31 14:08
:08/10/31 14:08  :SO906i
:SO906i  :☆☆☆
:☆☆☆
#20 [名前なし]
>>18レベルは全然高くないですよ。東大ですかf^_^;解けるか不安ですがよろしくお願いします。
>>19ありがとうございます。家についたらやってみます。
 :08/10/31 14:38
:08/10/31 14:38  :SH703i
:SH703i  :☆☆☆
:☆☆☆
#21 [ポチ▽・ェ・▽]
未だに自分の名前があることに感動(´;ω;`)ウッ…
なんだかんだで大学3年です(´・ω・`)
もうおじさんですか?
半分くらい知らない人ですね@@
久しぶりに問題解いてみるのもいいですね。
 :08/10/31 16:43
:08/10/31 16:43  :PC
:PC  :NhC/YFck
:NhC/YFck
#22 [名前なし]
ついにめんばー一覧に私がw
円周率のは見たことあるからすこしわかったけど、aの範囲とか知らないよ。もう全範囲でいいよwww
 :08/10/31 21:35
:08/10/31 21:35  :PC
:PC  :☆☆☆
:☆☆☆
#23 [あ]
おれも載ってる(´∀`)ありがと(^ω^)
>>19 が解けないw老化怖い\(^_^)/
>>20とりあえず志望校とかしらないから簡単目でどこでもでるだろう確率で
半径1の円に内接する正六角形の頂点をA1~A6とする
これらから任意に(無作為に)選んだ三点を頂点とする三角形の面積の期待値を求めよ
ただし2つ以上が一致するような三点が選ばれたとき三角形の面積は0とする
 :08/10/31 22:00
:08/10/31 22:00  :W61H
:W61H  :udyzDCGM
:udyzDCGM
#24 [あ]
>>19 1/2n+1<a<2n+1
かな?(^ω^;)
 :08/10/31 22:11
:08/10/31 22:11  :W61H
:W61H  :udyzDCGM
:udyzDCGM
#25 [名前なし]
 :08/10/31 22:53
:08/10/31 22:53  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs
#26 [名前なし]
綺麗に計算できた…
おっそー
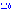
1/(2n+1)<a<2n+1
 :08/10/31 23:02
:08/10/31 23:02  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs
#27 [名前なし]
 :08/10/31 23:15
:08/10/31 23:15  :SH903i
:SH903i  :Zud35U0M
:Zud35U0M
#28 [名前なし]
>>23出題ありがとうございます。√3/4ですか?
>>191<a<n+1ですか?お二人と違うので間違ってそいだすが・・・
 :08/10/31 23:17
:08/10/31 23:17  :SH703i
:SH703i  :☆☆☆
:☆☆☆
#29 [名前なし]
SH903が2人‥誰だ?まめくんと遥?
23は合ってるね。19は違うよ(´ω`)
 :08/10/31 23:23
:08/10/31 23:23  :SO906i
:SO906i  :☆☆☆
:☆☆☆
#30 [あ]
 :08/10/31 23:26
:08/10/31 23:26  :W61H
:W61H  :udyzDCGM
:udyzDCGM
#31 [名前なし]
古いな(´ω`;)どんだけ過去問持ってんだ(^_^;)
 :08/10/31 23:29
:08/10/31 23:29  :SO906i
:SO906i  :☆☆☆
:☆☆☆
#32 [あ]
27年くらいw
本当に時間の無駄でした(^ω^;)
難しすぎの解いてもねorz
 :08/10/31 23:32
:08/10/31 23:32  :W61H
:W61H  :udyzDCGM
:udyzDCGM
#33 [名前なし]
>>27え~更にまだ計算ミスってる的な?(ノ_・。)
 :08/10/31 23:33
:08/10/31 23:33  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs
#34 [名前なし]
解きすぎだな^^;
てか、27年分の手に入れ方だけ知りたいw
 :08/10/31 23:39
:08/10/31 23:39  :SO906i
:SO906i  :☆☆☆
:☆☆☆
#35 [名前なし]
>>34俺も学校から拝借して25年くらいありますよw
25ヵ年買いたくなかったんで(゚⊿゚)
あさんとふわさんは数学何年分ぐらいやりました?
 :08/10/31 23:41
:08/10/31 23:41  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs
#36 [名前なし]
この携帯使いにくい(-_-;)
 :08/10/31 23:41
:08/10/31 23:41  :SO906i
:SO906i  :☆☆☆
:☆☆☆
#37 [名前なし]
あぁ赤本で東大の数学ってのあったな(´ω`)あれ買ったのか
10年分ぐらいやった(´・ω・`)
 :08/10/31 23:44
:08/10/31 23:44  :SO906i
:SO906i  :☆☆☆
:☆☆☆
#38 [名前なし]
こっちにしよ(´ω`)
赤本の東大の数学とやらはいくらだろうか(´`)
 :08/10/31 23:47
:08/10/31 23:47  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#39 [名前なし]
正解できて良かったです。
これはこのスレの方々にとっては簡単なレベルとなるのでしょうか?
19は全然わからないですf^_^;教えてもらえると助かります。
ちなみに阪大を目指しています(^0^)/
今日は寝ます。おやすみなさい
 :08/11/01 00:00
:08/11/01 00:00  :SH703i
:SH703i  :☆☆☆
:☆☆☆
#40 [名前なし]
ちょい易ぐらいじゃね?
教えてあげたいけどうつのめんどい(´`)
頑張って^^オヤスミ
 :08/11/01 00:04
:08/11/01 00:04  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#41 [名前なし]
2500円ぐらいか(´`)解答いらないし米村さんのとこから貰おう(´ω`)ノシ
 :08/11/01 00:08
:08/11/01 00:08  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#42 [あ]
東大の理系数学2300円
25ヶ年だけど25年前からってわけじゃないんだよね
5年分くらいさらっとやって飽きた\(^_^)/
mの二次の項の係数が正だし
判別式<0より
aの二次式<0
因数分解…答え
だったんだけど(^ω^;)
 :08/11/01 00:09
:08/11/01 00:09  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM
#43 [名前なし]
>>42mが整数って条件がなければそれでいいんだけど…
ガウス記号使おうとしながら悪戦苦闘中 笑
 :08/11/01 00:16
:08/11/01 00:16  :SH903i
:SH903i  :751DDxjA
:751DDxjA
#44 [名前なし]
m整数じゃねーかwwwwwwwwww
 :08/11/01 00:20
:08/11/01 00:20  :SH903i
:SH903i  :i1ismF56
:i1ismF56
#45 [名前なし]
米村さん、ありがとう(´ω`)
ひとまず、ありきたりに{n^2/(2n+1)}=lとでもおけば、与式が以下のように書ける
m^2+m>(m-l)a
で、放物線が直線の上にある条件を求めればいいかと
 :08/11/01 00:30
:08/11/01 00:30  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#46 [あ]
ほんとだwwwwww
ちょっと吊ってくる\(^_^)/
 :08/11/01 00:32
:08/11/01 00:32  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM
#47 [名前なし]
それかaについて解けば
0<a<(m^2+m)/{m-(n^2/2n+1)}となって…これで出るかね?
 :08/11/01 00:35
:08/11/01 00:35  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#48 [名前なし]
>>47は忘れてくれ('=';)
計算がとてつもない気がしてきた(´_`)
 :08/11/01 00:40
:08/11/01 00:40  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#49 [あ]
aを分離
m<l
m^2+m/l-m<a
m>lは符号とか逆
不等式左辺微分
微分の式が0
グラフ…m=lでわけてあるのに注意
結局mが整数であるの無視してルートが入った答えがorz
 :08/11/01 01:34
:08/11/01 01:34  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM
#50 [名前なし]
けっこう計算楽だった^ロ^;
解いたら、m=-{n/(2n+1)}で極大,m=nで極小かな
グラフ書いて、あとは条件に注意すれば、m>lのときの最小値とm<lのときの最大値出すだけか(´`)
 :08/11/01 02:13
:08/11/01 02:13  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#51 [名前なし]
ここまで読んでけど半分しか理解できんw
 :08/11/01 12:41
:08/11/01 12:41  :PC
:PC  :☆☆☆
:☆☆☆
#52 [名前なし]
出しっぱなしも微妙だし暇なので略解を書いときます
{n^2/(2n+1)}=l>0とおく
m^2+m>(m-l)a
xy平面で書きたいからm=xとしておきます。
放物線:y=x^2+x
直線:y=a(x-l)
放物線上の点のうち(m,m^2+m)が格子点となるような点が直線より上にある条件を求めればいいとわかる。
次に、直線は定点(l,0)を通るので定点から放物線へ引いた接線の傾きを考える
放物線上の点(p,p^2+p)[p>0]における接線Zは
Z:y=(2p+1)x-p^2
Zが点(l,0)を通るとき
p=l+(l^2+l)
ここで、{n^2/(2n+1)}=lを代入して整理すると
p=l+(l^2+l)=n
となる
したがって
Z:y=(2n+1)x-n^2
ゆえに、題意が成立するためには接線Zつまりは直線の傾きは2n+1より小さなければならない。さらに、放物線上で最も小さい格子点を考えれば、直線の傾きは0より大きなければならないことがわかる。(与式にm=0を代入してa>0でも大丈夫か?)
よって、0<a<2n+1■
 :08/11/01 22:33
:08/11/01 22:33  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#53 [名前なし]
一晩考えてもわからなかった(゚_゚やっぱしまだまだでしたね。解答ありがとうございました。一から修行し直してきます(゚-゚)ノシ
 :08/11/01 23:19
:08/11/01 23:19  :SH703i
:SH703i  :☆☆☆
:☆☆☆
#54 [あ]
格子点わからなかった(・ω・`)
 :08/11/01 23:34
:08/11/01 23:34  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM
#55 [名前なし]
いや、高2(?)だとしたらまだまだということはないと思うが…まぁまだ受験まで1年以上あるし頑張って(^o^)
 :08/11/01 23:40
:08/11/01 23:40  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#56 [名前なし]
a+b+c=2
このときa^2+b^2+c^2の最小値を求めよ
という問題皆さんならどう解きます?
定石とか知らない俺はとりあえずcをkと固定して右辺に移行しa^2+b^2の最小値をkで置きa^2+b^2+c^2を表して微分したんですが最善策とかないですかね?
 :08/11/02 00:35
:08/11/02 00:35  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#57 [名前なし]
些細やけど訂正
a+b+c=2
このときa^2+b^2+c^2の最小値を求めよ
という問題皆さんならどう解きます?
定石とか知らない俺はとりあえずcをkと固定して右辺に移行しa^2+b^2の最小値を証明してkで表し、a^2+b^2+c^2がkで表せたのでそれを微分したんですが最善策とかないですかね?
 :08/11/02 00:37
:08/11/02 00:37  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#58 [名前なし]
0になったwww
 :08/11/02 00:47
:08/11/02 00:47  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆
#59 [名前なし]
あっa^2+b^2の最小値の証明に使った方法拡張して
2/3 -α
2/3 -β
2/3 +α+β
にしてダイレクトに計算しても出来たorz
とりあえずまだ他に解法あるなら聞きたいです
 :08/11/02 00:52
:08/11/02 00:52  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#60 [名前なし]
 :08/11/02 00:54
:08/11/02 00:54  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#61 [名前なし]
 :08/11/02 00:59
:08/11/02 00:59  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#62 [名前なし]
数学はダメだw 3/4?
 :08/11/02 01:11
:08/11/02 01:11  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆
#63 [名前なし]
まぁ正しい答えは知らんが俺の結果とは違う
それはabcが存在してる?
 :08/11/02 01:19
:08/11/02 01:19  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#64 [名前なし]
逆だ、4/3だったorz
 :08/11/02 01:23
:08/11/02 01:23  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆
#65 [名前なし]
そうかと思ったよww
それなら俺の予想と一致する。
 :08/11/02 01:24
:08/11/02 01:24  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#66 [名前なし]
ん?これはネタだよな?ぇ
 :08/11/02 01:26
:08/11/02 01:26  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#67 [名前なし]
えーまたまたなんかやらかしたのか?orz
 :08/11/02 01:32
:08/11/02 01:32  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#68 [名前なし]
いや、これは解けばいいんだよね?
a^2+b^2+c^2≧ab+bc+ca
等号成立:a=b=c
∴a=b=c=2/3で最小値4/3■
となるよ\(^O^)/
 :08/11/02 01:34
:08/11/02 01:34  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#69 [名前なし]
そ、そんなあっさり…
これ見たら俺の2つはネタだわwwww
ありがとです
 :08/11/02 01:36
:08/11/02 01:36  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#70 [名前なし]
補足
x^2+y^2≧2|xy|,y^2+z^2≧2|yz|,z^2+x^2≧2|zx|より
x^2+y^2+z^2≧|xy|+|yz|+|zx|≧xy+yz+zx
∴x^2+y^2+z^2≧xy+yz+zx
これないと減点されるっぽいから一応書いとくΣ^)/
 :08/11/02 01:37
:08/11/02 01:37  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#71 [名前なし]
なんかごめん(・_・;)
頑張って\(^O^)/
 :08/11/02 01:38
:08/11/02 01:38  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#72 [名前なし]
いやいや勉強になりました。聞いて良かったです(笑
 :08/11/02 01:40
:08/11/02 01:40  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ
#73 [名前なし]
こっちが最初だったけど…
a^2+b^2+c^2=(a+b+c)^2-2(ab+bc+ca)=4-2(ab+bc+ca)
(ab+bc+ca)が最大となればよい→a^2+b^2+c^2=(ab+bc+ca)→あぁぁぁ\(^O^)/
腹へった
 :08/11/02 01:43
:08/11/02 01:43  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#74 [名前なし]
補足x,y,zになってる(@ω@)スマネ
頭がボーッとしてるみたいだなΣ^)ノシ
 :08/11/02 01:46
:08/11/02 01:46  :N902iX
:N902iX  :☆☆☆
:☆☆☆
#75 [ゆ ]
]
みんなどこ志望ですか?

 :08/11/05 09:45
:08/11/05 09:45  :SH706i
:SH706i  :1JL.4EJI
:1JL.4EJI
#76 [アーポ]
仲間に入れて下さい
九大医学部目指してます
高2です
 :08/11/06 00:43
:08/11/06 00:43  :W52SA
:W52SA  :M3tJtmsc
:M3tJtmsc
#77 [名前なし]
 :08/11/06 14:42
:08/11/06 14:42  :N902iX
:N902iX  :qVwIXhIU
:qVwIXhIU
#78 [ゆ ]
]
>>77すみません見てませんでした

ありがとうございます☆
私も入れてください

東北大・薬志望です。
 :08/11/06 15:27
:08/11/06 15:27  :SH706i
:SH706i  :GZMU9omw
:GZMU9omw
#79 [ストロングばにゃにゃん◆banana/0vM]
qω・`)
 :08/11/06 20:10
:08/11/06 20:10  :F905i
:F905i  :nipAR.42
:nipAR.42
#80 [名前なし]
東北薬も難関だしがんばってp(^^)q
このスレには東北志望いなかったのか(´`)
 :08/11/06 23:58
:08/11/06 23:58  :N902iX
:N902iX  :qVwIXhIU
:qVwIXhIU
#81 [アーポ]
名前なしさん⇒
ありがとうございます頑張ります
ゆさん⇒
初めまして
何歳ですか
 :08/11/07 00:17
:08/11/07 00:17  :W52SA
:W52SA  :qhxWIwD6
:qhxWIwD6
#82 [ゆ ]
]
>>名無しさん
ありがとうございます

頑張ります
>>アーポさん
18歳です☆浪人してます
お互い頑張りましょう

 :08/11/07 13:31
:08/11/07 13:31  :SH706i
:SH706i  :zpBz8JW2
:zpBz8JW2
#83 [アーポ]
ゆさん⇒
やっぱ医歯薬系は難しいですよね
いつ頃から薬学部を目指したんですか
 :08/11/07 19:30
:08/11/07 19:30  :W52SA
:W52SA  :qhxWIwD6
:qhxWIwD6
#84 [名前なし]
明日は即応オープン
夏から比べて対して伸びてる気がしないけど…
がんばるぜー(`・ω・)
 :08/11/07 19:45
:08/11/07 19:45  :F703i
:F703i  :☆☆☆
:☆☆☆
#85 [ゆ ]
]
>>アーポさん
んーと、高一くらいですねー☆
アーポさんは医学部ですよね
すごいです

成績とかいい感じですか?
 :08/11/07 22:00
:08/11/07 22:00  :SH706i
:SH706i  :zpBz8JW2
:zpBz8JW2
#86 [アーポ]
名前なしさん⇒
頑張って下さい
ゆさん⇒
成績はあまり…笑
夏に受けた進研模試でどこの医学部もE判定でした
夏ぐらいから本気で勉強始めてます
部活でインターハイに出場して、それを節目に練習は1日おきに参加させてもらう形にして、11月末までの大会までは両立で頑張ってます
その大会が終われば、もう息抜き程度に部活行こうと思ってます
モチベーションはMAXなんで、時間があれば必死で勉強してますよ
この間また進研模試があったんですが、それでちょっとでも判定がよくなってたら、精神安定剤にはなりそうなんですけど…笑
 :08/11/08 06:49
:08/11/08 06:49  :W52SA
:W52SA  :5mJZGAgM
:5mJZGAgM
#87 [名前なし]
ちょww
進研模試はないww
駿台とか受けたほうがいい進研ごときでE判なら
部活やめてから勉強するか部活をしながら、医歯薬以外のとこ目指せよ
言っちゃ悪いが
受かる可能性は0だ
2浪ぐらいしてやっと
1%の可能性がでるか
でないかぐらいだろ
 :08/11/08 08:50
:08/11/08 08:50  :SH904i
:SH904i  :RDGybVNI
:RDGybVNI
#88 [ゆ ]
]
あれ、進研模試って高二でも判定出るっけ?(・ω・)
私も高三の時ずーっとE判でした

でも浪人してから一気にあがってAとかB取るようになったよ

やっぱやる気が大事なんだと思います

高二なんだから必死でやれば来年までには判定上がる可能性大だと思いますよ

(なんか自分が受かってから言えって話だけど
笑)
お互い頑張ろう

 :08/11/08 09:15
:08/11/08 09:15  :SH706i
:SH706i  :rCWSZFgI
:rCWSZFgI
#89 [あ]
浪人したら一気にあがるけど最後は去年+1~2段階だった気がする
薬ならセンター9割弱くらいに詰まってくるだろうし気をつけた方が…(・ω・`;)
医学部なら進研模試より駿台とかがいいと思うけどまずは進研模試でAとかBとかとれないと駿台にフルボッコにされる\(^_^)/
 :08/11/08 11:00
:08/11/08 11:00  :W61H
:W61H  :eXEGNuXc
:eXEGNuXc
#90 [ゆ ]
]
>>あさん
ありがとうございます

実際今の段階で波があるんで気抜かないで頑張ります
 :08/11/08 15:41
:08/11/08 15:41  :SH706i
:SH706i  :rCWSZFgI
:rCWSZFgI
#91 [ゆーたろ◆iP9cG5.1Bg]
ベネ駿マーク11月みんなどんくらいとった?
 :08/11/08 19:05
:08/11/08 19:05  :F904i
:F904i  :awcqyrWQ
:awcqyrWQ
#92 [アーポ]
名前なしさん⇒
本当に厳しい事はよく分かっています
今の状況で可能性が0だと言われても仕方がありません
でも私は絶対に合格してみせます
厳しいお言葉本当にありがとうございます
必死こいて頑張ります
ゆさん⇒
励ましのお言葉本当にありがとうございます一緒に頑張りましょう
なんだか頑張っている人に出会うと、ますますやる気が上がりますね
あさん⇒
駿台も河合塾のやつも受けた事あります
やっぱり進研より全然難しかったです
これから模試もたくさん受けていこうと思ってます
どうしても焦っちゃって自分の実力が出せない事が多いんですよ
 :08/11/08 19:23
:08/11/08 19:23  :W52SA
:W52SA  :5mJZGAgM
:5mJZGAgM
#93 [青◆RINGO..uIA]
オープン数学微妙だ。
半分行かなかったかもな…
 :08/11/08 21:23
:08/11/08 21:23  :SH903i
:SH903i  :6PGo3A1c
:6PGo3A1c
#94 [青◆RINGO..uIA]
現役が悪くて採点甘くなることを祈る。
ノシ
 :08/11/08 21:24
:08/11/08 21:24  :SH903i
:SH903i  :6PGo3A1c
:6PGo3A1c
#95 [ゆ ]
]
>>アーポさん
受かると信じて頑張りましょう

ポジティブな気持ち大事です

>>青Ringoさん
お疲れ様です☆私も明日オープンです

お互い頑張りましょう
 :08/11/08 23:48
:08/11/08 23:48  :SH706i
:SH706i  :rCWSZFgI
:rCWSZFgI
#96 [ジャス]
浪人してセンターは10%近く上がったし、偏差値も15くらい上がったけど正直一橋受かる自信は100%じゃない。
でもこれだけは言える。
現役だろうが浪人だろうが現実はきちんと見ろ。
むやみやたらに医歯薬にこだわるのは良くない。
事実、医学部の半分程度が2浪だ。
今、1浪だけどもう1年勉強しなきゃならないとなると発狂するわ
 :08/11/09 00:58
:08/11/09 00:58  :SO902i
:SO902i  :DBrdPVfc
:DBrdPVfc
#97 [名前なし]
あぁ今日もか(´~`;)
まぁ、受かりたいなら1年ぐらい本気で勉強しろという話だろ(;´・`)
 :08/11/09 01:48
:08/11/09 01:48  :SH906i
:SH906i  :t4CXjZtc
:t4CXjZtc
#98 [アーポ]
青◆Ringoさん⇒
オープンお疲れ様です
ゆさん⇒
自分の努力次第ですよね後1年程、後悔しないように必死に頑張ります
ジャスさん⇒
名前なしさん⇒
医学部の厳しさを改めて思いしらされます
人よりも出遅れている分、努力し続けなきゃですね
 :08/11/09 07:16
:08/11/09 07:16  :W52SA
:W52SA  :dI58wLAU
:dI58wLAU
#99 [名前なし]
2年だけど帝医はあきらめなさい
そこからの逆転は不可能
浪人して駅弁医受かればいいほうだろ
15あがったってどんだけひどかったんだよww
でも、成功例です
浪人してもあがると限らない
改めて考えなおしたほうかいいよ
学校は、進学校なの?
 :08/11/09 08:03
:08/11/09 08:03  :PC
:PC  :SSBecYBA
:SSBecYBA
#100 [アーポ]
進学校です
 :08/11/09 08:25
:08/11/09 08:25  :W52SA
:W52SA  :dI58wLAU
:dI58wLAU
#101 [青◆RINGO..uIA]
進学校とか自称のとこもあるからな…疑ってるわけではないが
今年のオープンは何か…ね。現役と浪人の立場の違いによるものなのかただ難易度の問題なのか…
はぁ

 :08/11/09 17:54
:08/11/09 17:54  :SH903i
:SH903i  :YuR98opI
:YuR98opI
★コメント★
←次 | 前→
 トピック
トピック
C-BoX E194.194


 :08/10/29 00:38
:08/10/29 00:38  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg :08/10/29 00:39
:08/10/29 00:39  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg :08/10/29 00:39
:08/10/29 00:39  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg :08/10/29 00:40
:08/10/29 00:40  :SO906i
:SO906i  :d.IiIxMg
:d.IiIxMg ]
] :08/10/29 00:49
:08/10/29 00:49  :P905i
:P905i  :91Mltsbg
:91Mltsbg :08/10/29 01:16
:08/10/29 01:16  :SO902i
:SO902i  :diGJk4Ss
:diGJk4Ss :08/10/29 01:23
:08/10/29 01:23  :P703i
:P703i  :oZ762SKI
:oZ762SKI :08/10/29 10:24
:08/10/29 10:24  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆ :08/10/29 10:59
:08/10/29 10:59  :N902i
:N902i  :rsnfemGo
:rsnfemGo :08/10/29 21:37
:08/10/29 21:37  :SO903i
:SO903i  :iWa/ynxU
:iWa/ynxU :08/10/29 21:39
:08/10/29 21:39  :SO903i
:SO903i  :iWa/ynxU
:iWa/ynxU :08/10/29 22:20
:08/10/29 22:20  :P903i
:P903i  :V0FRtt76
:V0FRtt76 :08/10/29 22:45
:08/10/29 22:45  :SH903i
:SH903i  :t89fHafE
:t89fHafE :08/10/30 20:24
:08/10/30 20:24  :F703i
:F703i  :☆☆☆
:☆☆☆ :08/10/30 23:21
:08/10/30 23:21  :SH703i
:SH703i  :☆☆☆
:☆☆☆ :08/10/31 06:46
:08/10/31 06:46  :W61H
:W61H  :udyzDCGM
:udyzDCGM :08/10/31 12:09
:08/10/31 12:09  :SH703i
:SH703i  :☆☆☆
:☆☆☆ :08/10/31 13:58
:08/10/31 13:58  :W61H
:W61H  :udyzDCGM
:udyzDCGM :08/10/31 14:08
:08/10/31 14:08  :SO906i
:SO906i  :☆☆☆
:☆☆☆ :08/10/31 14:38
:08/10/31 14:38  :SH703i
:SH703i  :☆☆☆
:☆☆☆ :08/10/31 16:43
:08/10/31 16:43  :PC
:PC  :NhC/YFck
:NhC/YFck :08/10/31 21:35
:08/10/31 21:35  :PC
:PC  :☆☆☆
:☆☆☆ :08/10/31 22:00
:08/10/31 22:00  :W61H
:W61H  :udyzDCGM
:udyzDCGM :08/10/31 22:11
:08/10/31 22:11  :W61H
:W61H  :udyzDCGM
:udyzDCGM :08/10/31 22:53
:08/10/31 22:53  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs
 :08/10/31 23:02
:08/10/31 23:02  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs :08/10/31 23:15
:08/10/31 23:15  :SH903i
:SH903i  :Zud35U0M
:Zud35U0M :08/10/31 23:17
:08/10/31 23:17  :SH703i
:SH703i  :☆☆☆
:☆☆☆ :08/10/31 23:23
:08/10/31 23:23  :SO906i
:SO906i  :☆☆☆
:☆☆☆ :08/10/31 23:26
:08/10/31 23:26  :W61H
:W61H  :udyzDCGM
:udyzDCGM :08/10/31 23:29
:08/10/31 23:29  :SO906i
:SO906i  :☆☆☆
:☆☆☆ :08/10/31 23:32
:08/10/31 23:32  :W61H
:W61H  :udyzDCGM
:udyzDCGM :08/10/31 23:33
:08/10/31 23:33  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs :08/10/31 23:39
:08/10/31 23:39  :SO906i
:SO906i  :☆☆☆
:☆☆☆ :08/10/31 23:41
:08/10/31 23:41  :SH903i
:SH903i  :ovG04jGs
:ovG04jGs :08/10/31 23:41
:08/10/31 23:41  :SO906i
:SO906i  :☆☆☆
:☆☆☆ :08/10/31 23:44
:08/10/31 23:44  :SO906i
:SO906i  :☆☆☆
:☆☆☆ :08/10/31 23:47
:08/10/31 23:47  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 00:00
:08/11/01 00:00  :SH703i
:SH703i  :☆☆☆
:☆☆☆ :08/11/01 00:04
:08/11/01 00:04  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 00:08
:08/11/01 00:08  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 00:09
:08/11/01 00:09  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM :08/11/01 00:16
:08/11/01 00:16  :SH903i
:SH903i  :751DDxjA
:751DDxjA :08/11/01 00:20
:08/11/01 00:20  :SH903i
:SH903i  :i1ismF56
:i1ismF56 :08/11/01 00:30
:08/11/01 00:30  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 00:32
:08/11/01 00:32  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM :08/11/01 00:35
:08/11/01 00:35  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 00:40
:08/11/01 00:40  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 01:34
:08/11/01 01:34  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM :08/11/01 02:13
:08/11/01 02:13  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 12:41
:08/11/01 12:41  :PC
:PC  :☆☆☆
:☆☆☆ :08/11/01 22:33
:08/11/01 22:33  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/01 23:19
:08/11/01 23:19  :SH703i
:SH703i  :☆☆☆
:☆☆☆ :08/11/01 23:34
:08/11/01 23:34  :W61H
:W61H  :OxKJAeeM
:OxKJAeeM :08/11/01 23:40
:08/11/01 23:40  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/02 00:35
:08/11/02 00:35  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 00:37
:08/11/02 00:37  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 00:47
:08/11/02 00:47  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆ :08/11/02 00:52
:08/11/02 00:52  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 00:54
:08/11/02 00:54  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 00:59
:08/11/02 00:59  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 01:11
:08/11/02 01:11  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆ :08/11/02 01:19
:08/11/02 01:19  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 01:23
:08/11/02 01:23  :SO905iCS
:SO905iCS  :☆☆☆
:☆☆☆ :08/11/02 01:24
:08/11/02 01:24  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 01:26
:08/11/02 01:26  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/02 01:32
:08/11/02 01:32  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 01:34
:08/11/02 01:34  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/02 01:36
:08/11/02 01:36  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 01:37
:08/11/02 01:37  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/02 01:38
:08/11/02 01:38  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/02 01:40
:08/11/02 01:40  :SH903i
:SH903i  :ikEm8gjQ
:ikEm8gjQ :08/11/02 01:43
:08/11/02 01:43  :N902iX
:N902iX  :☆☆☆
:☆☆☆ :08/11/02 01:46
:08/11/02 01:46  :N902iX
:N902iX  :☆☆☆
:☆☆☆ ]
]
 :08/11/05 09:45
:08/11/05 09:45  :SH706i
:SH706i  :1JL.4EJI
:1JL.4EJI :08/11/06 00:43
:08/11/06 00:43  :W52SA
:W52SA  :M3tJtmsc
:M3tJtmsc :08/11/06 14:42
:08/11/06 14:42  :N902iX
:N902iX  :qVwIXhIU
:qVwIXhIU ]
] :08/11/06 15:27
:08/11/06 15:27  :SH706i
:SH706i  :GZMU9omw
:GZMU9omw :08/11/06 20:10
:08/11/06 20:10  :F905i
:F905i  :nipAR.42
:nipAR.42 :08/11/06 23:58
:08/11/06 23:58  :N902iX
:N902iX  :qVwIXhIU
:qVwIXhIU :08/11/07 00:17
:08/11/07 00:17  :W52SA
:W52SA  :qhxWIwD6
:qhxWIwD6 ]
]

 :08/11/07 13:31
:08/11/07 13:31  :SH706i
:SH706i  :zpBz8JW2
:zpBz8JW2 :08/11/07 19:30
:08/11/07 19:30  :W52SA
:W52SA  :qhxWIwD6
:qhxWIwD6 :08/11/07 19:45
:08/11/07 19:45  :F703i
:F703i  :☆☆☆
:☆☆☆ ]
] すごいです
すごいです
 :08/11/07 22:00
:08/11/07 22:00  :SH706i
:SH706i  :zpBz8JW2
:zpBz8JW2 :08/11/08 06:49
:08/11/08 06:49  :W52SA
:W52SA  :5mJZGAgM
:5mJZGAgM :08/11/08 08:50
:08/11/08 08:50  :SH904i
:SH904i  :RDGybVNI
:RDGybVNI ]
] でも浪人してから一気にあがってAとかB取るようになったよ
でも浪人してから一気にあがってAとかB取るようになったよ やっぱやる気が大事なんだと思います
やっぱやる気が大事なんだと思います 高二なんだから必死でやれば来年までには判定上がる可能性大だと思いますよ
高二なんだから必死でやれば来年までには判定上がる可能性大だと思いますよ
 笑)
笑)
 :08/11/08 09:15
:08/11/08 09:15  :SH706i
:SH706i  :rCWSZFgI
:rCWSZFgI :08/11/08 11:00
:08/11/08 11:00  :W61H
:W61H  :eXEGNuXc
:eXEGNuXc ]
]
 :08/11/08 15:41
:08/11/08 15:41  :SH706i
:SH706i  :rCWSZFgI
:rCWSZFgI :08/11/08 19:05
:08/11/08 19:05  :F904i
:F904i  :awcqyrWQ
:awcqyrWQ :08/11/08 19:23
:08/11/08 19:23  :W52SA
:W52SA  :5mJZGAgM
:5mJZGAgM :08/11/08 21:23
:08/11/08 21:23  :SH903i
:SH903i  :6PGo3A1c
:6PGo3A1c :08/11/08 21:24
:08/11/08 21:24  :SH903i
:SH903i  :6PGo3A1c
:6PGo3A1c ]
] ポジティブな気持ち大事です
ポジティブな気持ち大事です

 お互い頑張りましょう
お互い頑張りましょう
 :08/11/08 23:48
:08/11/08 23:48  :SH706i
:SH706i  :rCWSZFgI
:rCWSZFgI :08/11/09 00:58
:08/11/09 00:58  :SO902i
:SO902i  :DBrdPVfc
:DBrdPVfc :08/11/09 01:48
:08/11/09 01:48  :SH906i
:SH906i  :t4CXjZtc
:t4CXjZtc :08/11/09 07:16
:08/11/09 07:16  :W52SA
:W52SA  :dI58wLAU
:dI58wLAU :08/11/09 08:03
:08/11/09 08:03  :PC
:PC  :SSBecYBA
:SSBecYBA :08/11/09 08:25
:08/11/09 08:25  :W52SA
:W52SA  :dI58wLAU
:dI58wLAU
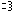
 :08/11/09 17:54
:08/11/09 17:54  :SH903i
:SH903i  :YuR98opI
:YuR98opI トピック
トピック


